Hi everyone, I'm hosting the 581st Carnival of Space where we assemble the best in space science and astronomy reporting. If you have a related website or blog, please consider joining us. Here is the fantastic lineup for this week!
Photon Fishing
Monday, October 8, 2018
Carnival of Space #581
Hi everyone, I'm hosting the 581st Carnival of Space where we assemble the best in space science and astronomy reporting. If you have a related website or blog, please consider joining us. Here is the fantastic lineup for this week!
Thursday, September 6, 2018
Support for Magnetic Complexity in Cataclysmic Variables
Cataclysmic variables (CVs) are binary systems consisting of a white dwarf and a secondary "normal" star. Material from the secondary star gets stripped away and forms an accretion disk around the white dwarf (see Figure 1). Astronomers observe variations in brightness of the system due to activity in the accretion disk.
 |
| Figure 1. Typical Cataclysmic Variable system. Credit NASA |
One observable characteristic of a CV is its orbital period, the amount of time it takes one object to go around the other. An interesting fact to come out of studying CVs over many decades is that there is a paucity of orbital periods between roughly 2 and 3 hours (see Figure 2). This so-called period gap has been a mystery to astronomers for since the late 1970s.
 |
| Figure 2. Histogram illustrating the period gap between roughly 2 and 3 hours Credit Carraffo et al. 2018 |
There are some ideas about why such a period gap may exist. The prevailing hypothesis is centered on the notion of loss of angular momentum. The
standard explanation is that at less than 2 hours the loss of angular momentum
is dominated by gravitational radiation while at greater than 3 hours
it is dominated by magnetic braking. Let's pause for a moment to consider these terms.
Gravitational radiation (a.k.a., gravitational waves) is a byproduct of Einstein's theory of general relativity (GR). GR views gravity not as a force, but instead a result of the curvature of space created by objects with mass. When you have two massive bodies orbiting each other rapidly (i.e., a CV system), they create ripples in space. Such ripples were detected for the first time in 2015 to great fanfare. A result of gravitational radiation is that energy, and thus angular momentum, is lost from the binary system.
Magnetic braking is another way for stars to lose angular momentum. Stars are spinning balls of plasma (ionized gas) that give rise to magnetic fields around themselves. The magnetic field lines can strip away ions in the star's atmosphere and carry them away. Again, this mass loss leads to a loss in angular momentum. This phenomena can be greatly exacerbated by stars with strong magnetic fields.
Back to CVs, remember that astronomers think that gravitational radiation dominates systems with periods less than 2 hours and magnetic braking is responsible for those above 3 hours. So why the period gap? The proposed reason for
the gap is that around a period of 3 hours the magnetic breaking "turns off", the
secondary star contracts and its orbit shrinks resulting in a quicker
(< 2 hour) period. However, there is a dearth of evidence supporting this idea of an interruption of the magnetic field at about 3 hours. An alternative explanation offered by Taam & Spruit (1989) suggests that as the secondary star's rotation decreases, its magnetic complexity increases which leads to less effective loss of angular momentum. In other words, the magnetic field lines get gnarly and cannot shuttle the mass away in an orderly fashion.
In a recent study, Garraffo et al (2018). studied the CV period gap by attempting to model this magnetic behavior using Zeeman-Doppler imaging (ZDI). This also deserves some explanation. The Zeeman effect is the observation that individual spectral lines can be split into multiple parts in the presence of a strong magnetic field. When this effect is observed for a system over time, it can be used to essential re-create the structure of the underlying magnetic field (see Figure 3).
 |
| Figure 3. Zeeman-Doppler imaging reconstruction of a young star's magnetic field. Credit Wikipedia |
In the models that Garraffo et al. (2018) created, they showed that surface magnetic complexity did indeed increase along with the decrease in orbital period. These results support the idea that magnetic complexity can suppress mass loss. Consequently, this reduction in the loss of angular momentum could result in the cessation of accretion to the primary. Recall that the accretion disk is how astronomers observe CVs, so when it is "off" no observations could be made. This is a very plausible explanation for the existence of the period gap. As the system continues to lose angular momentum, eventually the components are in close enough proximity for gravitational radiation to take over. As always, more studies will be needed to confirm if magnetic complexity is indeed responsible for the infamous CV period gap.
Thursday, August 30, 2018
One Disk to Rule Them All
 |
| Figure 1. A typical dwarf nova. Credit NASA via www.skyandtelescope.com |
SS Cyg is a well studied variable star system in the constellation Cygnus the swan. Specifically, it is a special type of cataclysmic variable called dwarf novae (DNe). DNe consist of a binary system made up of a primary white dwarf that every so often siphons off material from its low-mass companion that has overfilled its Roche Lobe. This material forms an accretion disk that swirls around the primary star. It is this accretion disk that will occasionally brighten across a variety of wavelengths. These "brightenings" are associated with outbursts and, along with DNe, are observed across a variety of astrophysical phenomena such as X-ray binaries (XRBs) and Active Galactic Nuclei (AGN). Although these are widely different phenomena, astronomers have evidence to support the idea that they share the same underlying accretion disk that gives rise to the outbursts. Subsequently, these are interesting targets for research since studying any of these objects could shed light on all the others.
There have been several studies of that give credence to the notion of an accretion disk connection between CVs, XRBs, and AGN. For example, all three objects have demonstrated that increases in brightness are correlated with increases in variability. This suggests mass transfer to the accretion disk resulting in the aforementioned increases in both brightness and variability. Furthermore, fluctuations in the outer, cooler parts of the disk are hypothesized to travel inwards towards hotter regions. This leads to emission of soft photons (lower energy) from the cooler areas of the disk before hard photons (higher energy) from the hotter, inner regions of the disk. Subsequently, there have been X-ray studies where soft photons arrive at astronomers' detectors slightly before hard photons, a so-called 'hard/positive' time lag. Because this phenomena presumably requires mass transfer, it is only observed during an outburst.
However, what about periods of no mass transfer? There have been reports of 'soft/negative' time lags in CVs, meaning that the hard photons arrive before the soft ones. There is debate over the cause of this soft lag. One explanation is that emission from the source (white dwarf) lights up the disk, which in turn creates a reflection spectrum. However, this idea suffers from the report that such a spectrum would lie outside the binary orbit. An alternative explanation is that the photons from the white dwarf are thermally reprocessed in the disk, leading to hard photons being emitted from the accretion disk before soft ones (i.e., a soft/negative lag, see Figure 2).
 |
| Figure 2. Diagram showing emission of photons from the white dwarf being reprocessed in the disk. Since the higher energy/hard (u) photons are closer to the source, they get reprocessed before the lower energy/soft (r) photons resulting in the 'soft lag'. Credit Aranzana et al. 2018 |
The purpose of the study was to gather more evidence that could improve upon or rule out either of the models. SS Cyg was chosen as an optical target because it is one of the brightest DNe during quiescence (no activity). Researchers used the 4.2 meter William Herschel Telescope located in the Canary Islands, Spain over the course of two nights to take images using SDSS filters Ultraviolet (u), Green (g), and Red (r). In astronomy, color is typically represented by combining two filters. For example, r & u is the combination of the red and ultraviolet filters. Figure 3 shows the results for the three different color combinations averaged over both nights. At a frequency of 4 x 10-3 Hz there is about a -6 second time lag in the g & u combination and -4 second time lag in the r & u combination.
 |
| Figure 3. SS Cyg during quiescence demonstrating a significant -4 second time lag for r&u and -6 second time lag for g&u at 0.004 Hz. The r&g Credit Aranzana et al. 2018 |
Labels:
AAVSO,
accretion disk,
Active Galactic Nuclei,
AGN,
astronomy,
cataclysmic variable,
DNe,
dwarf novae,
MNRAS,
photon,
Roche Lobe,
SS Cyg,
variable,
white dwarf,
William Herschel Telescope,
X-ray binary,
XRB
Tuesday, August 28, 2018
Frosty the Protoplanetary Disk Snowline
A key idea in astronomy is that stars form from collapsing clouds of gas and dust. The left over materials from the star formation swirl around the star in a flat plane known as a protoplanetary disk. Planets are thought to build up from the progressive clumping together of this matter, an idea known as the core accretion model. An important dividing line in the protoplanetary disk is the snowline, the point at which gas molecules freeze out onto grains of dust. More specifically, the water snowline is thought to be very important because of the number of planets that have high compositions of water ice. A planet's bulk composition is presumably highly dependent on the location of its formation relative to this snowline.
This transition from gas to water ice happens when the temperature drops below 100 K. For most protoplanetary disks, this means that the water snowline is only a few astronomical units (AU) its star, making it difficult to observe. However, young forming stars sometimes have outbursts as they accrete matter. These bursts heat up the surrounding disk and cause ice to turn to gas. Following the burst, the dust cools relatively quickly, but it takes longer for molecules to freeze back onto those dust grains. The result is that this temporarily moves the snowline out further. This has been previously observed indirectly using a carbon monoxide isotope (C18O) as a marker. CO was used as marker because water is harder to detect with spectroscopy and CO's volatility is similar to water.
In a recent study accepted for publication in the Astrophysical Journal Letters, researchers investigated V883 Ori, a young 1.3 solar mass protostar with a surrounding disk and evidence for an ongoing burst (i.e., its near-IR spectrum is similar to other protostars undergoing outburst). Similar to carbon monoxide, methanol (CH3OH) can be used as a proxy for water because of their similar characteristics. As party of an ongoing survey to study such disks, the researchers discovered both C18O and CH3OH using a combination of the Very Large Array (VLA) and the Atacama Large Millimeter/submillimeter Array (ALMA). They found that the methanol was thermally desorbed (i.e., released from the dust), implying that the water snowline may reside at about 100 AU.
As shown in Figure 1, the researchers used a moment map to display the kinematics of their results. In the top half of the figure, the blue and red contours correspond to the blue- and redshifted emission transitions that were detected for each molecule. The velocity gradient shown is what would be expected for a rotating disk. In the bottom half of the figure, the radial profiles are shown indicating a water snowline around 100 AU.
The researchers state that it is not possible to determine the exact location of the water snowline without a better physical model of the protoplanetary disk. This is due to the fact that while methanol's gas phase is influenced by the temperature in the disk, its presence is also affected by radiation, which can dissociate the molecules. Therefore, material in the disk shielding the methanol from radiation plays a factor in how far out the water snowline may actually extend. The researchers suggest more detailed modeling of the disk as well as using other molecular tracers to further constrain their result. The chemistry around forming stars is complex and difficult to study due to its proximity to the star itself. Therefore, young systems undergoing outbursts such as V883 Ori will continue to provide astronomers an invaluable opportunity to probe the processes that contribute to planet formation.
This transition from gas to water ice happens when the temperature drops below 100 K. For most protoplanetary disks, this means that the water snowline is only a few astronomical units (AU) its star, making it difficult to observe. However, young forming stars sometimes have outbursts as they accrete matter. These bursts heat up the surrounding disk and cause ice to turn to gas. Following the burst, the dust cools relatively quickly, but it takes longer for molecules to freeze back onto those dust grains. The result is that this temporarily moves the snowline out further. This has been previously observed indirectly using a carbon monoxide isotope (C18O) as a marker. CO was used as marker because water is harder to detect with spectroscopy and CO's volatility is similar to water.
In a recent study accepted for publication in the Astrophysical Journal Letters, researchers investigated V883 Ori, a young 1.3 solar mass protostar with a surrounding disk and evidence for an ongoing burst (i.e., its near-IR spectrum is similar to other protostars undergoing outburst). Similar to carbon monoxide, methanol (CH3OH) can be used as a proxy for water because of their similar characteristics. As party of an ongoing survey to study such disks, the researchers discovered both C18O and CH3OH using a combination of the Very Large Array (VLA) and the Atacama Large Millimeter/submillimeter Array (ALMA). They found that the methanol was thermally desorbed (i.e., released from the dust), implying that the water snowline may reside at about 100 AU.
As shown in Figure 1, the researchers used a moment map to display the kinematics of their results. In the top half of the figure, the blue and red contours correspond to the blue- and redshifted emission transitions that were detected for each molecule. The velocity gradient shown is what would be expected for a rotating disk. In the bottom half of the figure, the radial profiles are shown indicating a water snowline around 100 AU.
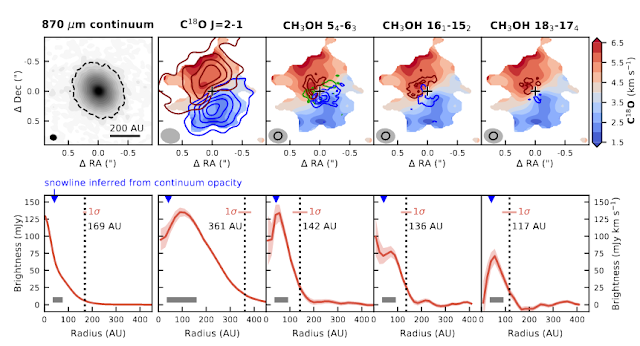 | |
| Figure 1. Top: Moment map showing the kinematics of V883 Ori; Bottom: Radial profile demonstrating the inferred snowline derived for each type of molecule detected Credit: Merel, L. R. et al. (2018) |
Friday, April 3, 2015
Binning
Binning groups pixels together which has the effect of
making the group appear as a bigger single pixel as shown in figure 1 below (Templeton
& Beck 2014). Binning is done to
decrease the resolution:
So by increasing the pixel size while keeping the focal
length constant, the resolution goes down.
This might seem backwards, but lower numbers imply higher resolution
since less of the sky is "landing" on each pixel creating a sharper image. The benefit
of binning is that you gain better sensitivity so you can do shorter exposures
(Templeton & Beck 2014). The
drawback is that you do lose some resolution so you have to be careful not to
blend close by stars together if you are trying to do accurate photometry
(Templeton & Beck 2014). Another
important thing to remember is that you have to redo all of your calibration
frames and test the linearity for each set of bins (Templeton & Beck
2014). In other words, a dark frame at
1x1 binning is not equivalent to a dark frame at 2x2 binning.
Figure 1. Examples of binning (Templeton & Beck
2014)
References
Templeton, M. & Beck, S. (2014), The CCD Guide to
Photometry Version 1.1, Cambridge, MA
Wednesday, February 18, 2015
Using Stellarium to Control a Telescope
One of the most awesome features of modern amateur telescopes is that they can connect with a computer to allow control by a wide assortment of software. Planetarium software is particularly cool because it enables you to simply click objects to direct your telescope to point at them. Although there are many planetarium software choices available that range from super fancy (and expensive!) to bare bones, my favorite is Stellarium. This is a free open source planetarium for your computer that is highly customizable. I like to use Stellarium in conjunction with Maxim DL to control my photometry sessions with TECMO. Maxim DL is the swiss army knife of telescope imaging software because it allows for control of the telescope, camera, dome, filters, focuser, etc. all through one program. However, the "All-Sky" planetarium view in Maxim DL is pretty paltry so that's why I opt to couple it with Stellarium for a more visually intuitive interface. There is lots of documentation on the internet about the basic use of Stellarium (start with their wiki), so this post will focus primarily on the aspect of telescope control. There is also plenty of documentation on this topic, but sometimes it can be confusing and I personally find it helpful to be able to follow a worked example.
This guide will assume that you have a computerized GOTO mount that is compatible, have already downloaded and installed Stellarium, and that you have the appropriate ASCOM drivers that make all this different software compatible. Although it is possible to directly control your telescope with Stellarium, I highly recommended also installing StellariumScope. This third party application acts as a server and extends the number of devices that can be controlled by Stellarium. If you're going to be doing a lot of imaging with your telescope, another tip is that you should update all the star catalogs in Stellarium. It comes with a base package of the brighter stars, but adding the additional catalogs really improves the accuracy of what you see in Stellarium compared with what see in your images. This can be done under Configuration window - Tools tab. Ok, now that you have all of your software installed and updated, it's time to connect the telescope.
Detailed instructions for this process can be found in the StellariumScope manual located in the Help Menu. Here is a brief synopsis: First, connect your telescope's mount to your computer (not necessary if you just want to try the simulator). The telescope will have to be properly aligned before you can successfully aim it with any third-party software. You will have to run Stellarium at least one time before proceeding to the next step. (1) Fire up StellariumScope and choose 'Select mount' near the top left of the window. If ASCOM is properly installed, you should see a new menu of your available telescopes. (2) For the purposes of this demonstration, I will be choosing the 'Simulator'. This is a good way to get a feel for the settings. (3) Next, choose 'Update Stellarium Configuration' and follow the prompts. This automatically selects the settings that enable StellariumScope to "talk" with Stellarium. (4) Finally, click the box next to 'Connect'.
So that's a basic walk-through of controlling your telescope. There's a lot more to learn to enhance your experience, but once you get through the start-up hurdle it should be smooth sailing. Please contact me if you have any questions about this demo.
This guide will assume that you have a computerized GOTO mount that is compatible, have already downloaded and installed Stellarium, and that you have the appropriate ASCOM drivers that make all this different software compatible. Although it is possible to directly control your telescope with Stellarium, I highly recommended also installing StellariumScope. This third party application acts as a server and extends the number of devices that can be controlled by Stellarium. If you're going to be doing a lot of imaging with your telescope, another tip is that you should update all the star catalogs in Stellarium. It comes with a base package of the brighter stars, but adding the additional catalogs really improves the accuracy of what you see in Stellarium compared with what see in your images. This can be done under Configuration window - Tools tab. Ok, now that you have all of your software installed and updated, it's time to connect the telescope.
Detailed instructions for this process can be found in the StellariumScope manual located in the Help Menu. Here is a brief synopsis: First, connect your telescope's mount to your computer (not necessary if you just want to try the simulator). The telescope will have to be properly aligned before you can successfully aim it with any third-party software. You will have to run Stellarium at least one time before proceeding to the next step. (1) Fire up StellariumScope and choose 'Select mount' near the top left of the window. If ASCOM is properly installed, you should see a new menu of your available telescopes. (2) For the purposes of this demonstration, I will be choosing the 'Simulator'. This is a good way to get a feel for the settings. (3) Next, choose 'Update Stellarium Configuration' and follow the prompts. This automatically selects the settings that enable StellariumScope to "talk" with Stellarium. (4) Finally, click the box next to 'Connect'.
At this point you should be connected with Stellarium. You will know that the setup was successful if you see the orange telescope reticle appear in Stellarium:
You may have to adjust your view in Stellarium in order to find the reticle. If you find it, you're good to go; if not, try going through the steps again and double-checking the manual. Assuming you're connected, it's time to play around. You'll notice on the StellariumScope figure above the 'Port Number' and 'Key' settings in the middle of the screen. The workhorse command here is slew which tells the telescope where you want it to point. Simply click the object you want to observe and then press 'Ctrl-1' (or whatever you choose to set it to) and watch the magic happen as the reticle moves across the screen to zero in on your target. If your telescope is properly aligned and connected, it will also be pointing at the desired target!
But wait, there's more...Another awesome feature is that you can enter in the specifications from your telescope and camera (or eyepiece) to allow Stellarium create the view you should be getting. This can help you confirm if you are, in fact, pointed at what you think you are. Here's how to do it: (1) In Stellarium, select 'Configuration' and then choose 'Oculars' under the 'Plug-ins' tab. Now you can enter all of the relevant information for you system such as aperture, focal length, chip size, pixel size, etc. I like to choose the option to have this plug-in load at start-up because I find it so invaluable. After configuring your settings, close out the menu and you will see the new menu at the top right of the screen (see image above). Let's say that I slew my simulator telescope to M37. If I want to go get a pretty good idea of what I can image with my 8 inch Celestron SCT coupled with an SBIG ST-8XE CCD, I can select the rectangular 'Image Sensor Frame' which zooms in gives a red outline of what should be visible. Of course, seeing conditions will affect the actual image. You may also notice that I have selected 'Ctrl-M' in Stellarium to switch to equatorial mode. If your CCD is aligned with the field of view oriented North-South, this will assist in matching what you see on the screen. Simply click the 'Image Sensor Frame' button again to zoom back out.
Saturday, November 22, 2014
Swan Song
Figure 1. Henrietta Swan Leavitt (Johnson 2005)
Henrietta Swan Leavitt was born on the Fourth of July in 1868 in Lancaster Massachusetts to George Roswell Leavitt and his wife, also named Henrietta Swan (Johnson 2005). The Leavitts were a family that valued education and scholarship (Johnson 2005). George was an ordained minister and his brother, Erasmus Darwin Leavitt, was the second president of the American Society of Mechanical Engineers and played a key part in the design of the Leavitt pumping engine at the Boston Water Works’ Chestnut Hill station (Johnson 2005). The Leavitts were a middle to upper-middle class family that found themselves living in Cambridge by 1880 (Johnson 2005). Their household was crowded as Henrietta’s siblings included George, Caroline, Mira, Martha, Roswell, and Darwin (Johnson 2005). Unfortunately, Mira and Roswell both passed away at very young ages due to childhood illnesses (Johnson 2005). The Leavitt household also included their Aunt Mary, a servant girl, and right next door was their grandfather (Johnson 2005).
In 1885 the Leavitts moved to Cleveland and later that year Henrietta enrolled at Oberlin College (Johnson 2005). However, she returned to Cambridge in 1888 to study at Radcliffe (Johnson 2005). There she took classes in Latin, Greek, modern languages, mathematics, physics, and astronomy (Johnson 2005). Interestingly, she only got a B in physics but did manage an A- in astronomy (Johnson 2005). Her only C was in German (Johnson 2005). She graduated in 1892 at the age of twenty-four with the equivalent of a bachelor of arts from Harvard for a man (Johnson 2005). In 1893, she volunteered at Harvard observatory (Singh 2004). At the time, the Harvard observatory was engaged in an extensive project to catalog the brightness of every star in the sky (Johnson 2005). In charge of this effort was a young physicist from the Massachusetts Institute of Technology named Edward Charles Pickering (Singh 2004).
Figure 2. Edward Charles Pickering (Johnson 2005).
Pickering was more than happy to put someone like Henrietta to work recording the magnitudes of stars (Nelson 2008). While this type of work is now done by machines, in the nineteenth century women were employed as a cost effective means of measuring, calculating, and recording observations of the photographs taken by the observatory’s telescope (Singh 2004). These human “computers” were paid only twenty-five cents an hour for six days of work per week and afforded a month’s vacation (Nelson 2008). Another one of the women at the observatory described the workroom as a “dark and dingy place, all cluttered up and smelling strong of oil,” in reference to the oil-burning fireplaces (Johnson 2005). Nevertheless, Henrietta managed to excel in her work at the Harvard observatory. Her hearing had gradually declined since birth, so this type of work was suited for her (Singh 2004). While fastidiously examining these photographic plates in her workroom, Henrietta Swan would make an incredible discovery that enabled measurement to distances beyond our galaxy and revolutionized modern astronomy.
Henrietta Leavitt’s work is embodied in what is now known as Henrietta’s Law. During the time of her employment at the observatory, one of the great questions in astronomy involved the cloud-like nebulae that shined in the night sky. Were these objects nearby and part of the Milky Way or were they distant galaxies? In particular, Henrietta was studying photographic plates of the Large and Small Magellanic clouds in search of variable stars, carefully plotting the change in magnitudes of certain stars with respect to others and determining the period, or length of time between one bright phase to the next (Johnson 2005). She was a variable star fiend, later writing that she was making “an extraordinary number” of discoveries (Johnson 2005). She published her findings in the Harvard observatory’s bulletin and made an immediate impression on the astronomical community (Johnson 2005). One astronomer noted that he could not keep of with the pace of Henrietta’s new discoveries (Johnson 2005). She eventually discovered and cataloged hundreds of variable stars in the Magellanic Clouds (Johnson 2005).
Miss Leavitt continued to amass new discoveries and report them in the Harvard circular. The sheer volume of her data accumulation would have been impressive enough, but this human computer was able to see something that the professional astronomers had missed. In 1908, one of her reports included a note that simply stated, “The brighter variables have the longer periods” (Leavitt et al. 1908). In her typical humble style, she was simply trying to relay the facts and not over-interpret the data. However, the implications were immediately obvious: because the stars she was observing were all in the Magellanic Clouds, they were all about the same distance from Earth (Mitchell 1976). If the correlation she uncovered was in fact correct, a star’s absolute brightness (luminosity) could be gleaned from determining its period. Then comparing this absolute luminosity with its apparent brightness will yield the distance (Mitchell 1976). Knowing the distance would then be a major piece of the puzzle to solve the great question about nebulae and whether or not they are beyond the Milky Way galaxy. More data was needed to confirm this hypothesis.
Unfortunately, soon after her report was published, she fell ill and returned to stay with her parents who were now in Wisconsin (Bartusiak 2009). Since was gone for so long and because Pickering so valued her work, a box of plates was shipped to her so she could examine them while recovering (Bartusiak 2009). She finally made it back to Harvard in 1910 after a year and half absence, but almost immediately had to leave again when father passed away (Bartusiak 2009). She eventually got back to the observatory and published her latest results in the 1912 Harvard Circular. The report boldly stated, “A remarkable relation between the brightness of these variables and the length of their periods will be noticed” (Leavitt et al. 1912). In other words, brighter stars have longer periods. The stars measured are known as Cepheid variables because the first of its type was found in the constellation Cepheus (Johnson 2005). This new Cepheid yardstick (i.e., Henrietta’s law) could be used to determine the relative distances between stars (Johnson 2005). Now all that was needed was the distance to the closest star in order to calibrate this yardstick.
The technique used to measure the distance to the closest stars is known as parallax (Johnson 2005). This involves measuring the angle to a star at a certain time and then measuring it again precisely six months later when the Earth is on the other side of the Sun (Johnson 2005). Stars that are relatively close will appear to move in relation to the further away background star similar to the way one’s extended thumb appears to move in relation to background objects when one alternately blinks his eyes. Although simple in theory, this technique is difficult to implement in practice due to the enormous distances of the stars and the precision instruments required to detect their motion (Johnson 2005). After several attempts, the American astronomer Henry Norris Russell used parallax to put the distance of the Small Magellanic Cloud at 80,000 light years, a truly mind blowing number at the time (Johnson 2005). Russell wrote to his colleague Ejnar Hertzsprung, “I had not thought of making the very pretty use you make of Miss Leavitt’s discovery about the relation between period and absolute brightness. There is of course a certain element of uncertainty about this, but I think it is a legitimate hypothesis” (Johnson 2005). Thanks to Henrietta Swan Leavitt, astronomy finally had a way to measure beyond the closest stars and determine if there were objects beyond the Milky Way.
Unfortunately, despite her invaluable contribution, Henrietta continued to toil away in obscurity as a glorified computer. This did not deter her efforts as she continued to not only amass data, but also provide details notes about biases and uncertainties. For example, she wrote about the uncertainty in her measurements, “It is evident that, owing to the small range of the variable and the difficulty of estimating the magnitude of so bright an object, the observations are not sufficiently precise to permit a further correction to the period” (Leavitt et al. 1914). Johnson (2005) wrote, “It was work to take pride in. Ph.D.s have been awarded for less.” Astronomer Harlow Shapley admired Henrietta’s work and used it to calibrate the size of the Milky Way in order to debate the theory of “island universes.” This was the idea that the Milky Way was just one of many galaxies throughout the universe. Of Henrietta, Shapley wrote, “Her discovery of the relation of period to brightness is destined to be one of the most significant results of stellar astronomy” (Johnson 2005). After he assumed leadership of the Harvard observatory following Pickering’s death, Shapley called Henrietta, “one of the most important women ever to touch astronomy.” Tragically, Henrietta would not live long enough to see all the fruits her discovery would be bear as she passed away on December 12, 1921 (Johnson 2005).
As a consequence, it is vitally important that Henrietta Swan Leavitt’s importance to the field of astronomy be recognized. According to Johnson (2005), Henrietta Swan Leavitt’s story has “slipped through the cracks.” Perhaps this is because she never married and died young (Johnson 2005). Another reason could be her solemn Puritanical nature. In her obituary, a colleague wrote:
“Miss Leavitt inherited, in a somewhat chastened form, the stern virtues of her puritan ancestors. She took life seriously. Her sense of duty, justice and loyalty was strong. For light amusements she appeared to care little. She was a devoted member of her intimate family circle, unselfishly considerate in her friendships, steadfastly loyal to her principles, and deeply conscientious and sincere in her attachment to her religion and church.” (Johnson 2005).
Henrietta accomplished her work during a time when astronomy was decidedly dominated by males. Even the scant praise she earned was somewhat hollow as it condescendingly described women as being adept at detailed work, but affirmed that more difficult think matters were best suited for men (Johnson 2005). Despite all of this, she endured unflinchingly and led the way for refining the astronomical yardstick. Unlike some of her colleagues, Henrietta left behind little in the form of personal writings that would give some clue as to her feelings about her status in the field. Instead, she left behind a wealth of data and meticulous notes that enabled other astronomers to unlock the mysteries of the universe. Even to this day, astronomers are still refining her period-luminosity relationship, particularly the influence of metallicity (Garcίa-Varela 2013).
The h-index is a way of quantifying an individual’s research impact. According to Harzing (2007), Henrietta is credited with authorship of thirty-nine articles and has received 319 citations for an average of 8.18 citations per paper giving her an h-index of 4. For comparison, Henry McEwen was an amateur astronomer during the same time period wrote 89 papers, received 1119 citations (12.57 citations per paper), giving him a h-index of 16 (McKim 2005 & Harzing 2007). This may paint Henrietta’s contribution as low until we look at the two Harvard observatory directors whose careers she most powerfully influenced: Pickering’s h-index of 28 and Shapley’s h-index of 30 are incredibly high. It is difficult, if not impossible, to assess Henrietta Swan Leavitt’s importance using traditional metrics. She was not technically an astronomer, but rather a “skilled laborer” at the observatory (Johnson 2005). Consequently, while she did submit her data in the observatory’s bulletin, she rarely submitted in the more prestigious astronomical journals. Nevertheless, she was undoubtedly an astronomer in the purest sense of the word: she took observations and looked for underlying phenomena to predict future astronomical events. She understood that the discovery was the important thing, not the discoverer (Johnson 2005). Everyone interested in astronomy should know not only about the role Cepheid variables on the distance ladder, but also about the remarkable woman who unlocked their secret.
References
Bartusiak, M. 2009, Natural History, 118, 14-17
Burleigh, R. 2013, Look Up!, (New York: Simon & Schuster)
Garcίa-Varela et al. 2013, MNRAS, 431, 2278-2284
HARVARDweb: http://dasch.rc.fas.harvard.edu/telescopes.php accessed 29 August 2014
Harzing, A. W. 2007, http://www.harzing.com/pop.htm
Johnson, G. 2005, Miss Leavitt’s Stars, (New York: W.W. Norton & Co.)
Leavitt, H. et al. 1908, Annals of Harvard College Observatory, 60, 87-108
Leavitt, H. et al. 1912, Harvard College Observatory Circular, 173, 1-3
Leavitt, H. et al. 1913, Harvard College Observatory Circular, 179, 1-4
Leavitt, H. et al. 1914, Harvard College Observatory Circular, 186, 1-4
McKim, R. 2005, JBAA, 115, 13
Mitchell, H. 1976, The Physics Teacher, 14, 162-167
Nelson, S. 2008, Nature, 455, 36-37
Singh, S. 2004, New Scientist, 184, 54-55
Figure 3. Henrietta Swan Leavitt, at work for the Harvard College Observatory, Cambridge, Massachusetts (Bartusiak 2009)
Henrietta Leavitt’s work is embodied in what is now known as Henrietta’s Law. During the time of her employment at the observatory, one of the great questions in astronomy involved the cloud-like nebulae that shined in the night sky. Were these objects nearby and part of the Milky Way or were they distant galaxies? In particular, Henrietta was studying photographic plates of the Large and Small Magellanic clouds in search of variable stars, carefully plotting the change in magnitudes of certain stars with respect to others and determining the period, or length of time between one bright phase to the next (Johnson 2005). She was a variable star fiend, later writing that she was making “an extraordinary number” of discoveries (Johnson 2005). She published her findings in the Harvard observatory’s bulletin and made an immediate impression on the astronomical community (Johnson 2005). One astronomer noted that he could not keep of with the pace of Henrietta’s new discoveries (Johnson 2005). She eventually discovered and cataloged hundreds of variable stars in the Magellanic Clouds (Johnson 2005).
Figure 4: 1-Inch Cooke Telescope used to take photographs (HARVARDweb)
Miss Leavitt continued to amass new discoveries and report them in the Harvard circular. The sheer volume of her data accumulation would have been impressive enough, but this human computer was able to see something that the professional astronomers had missed. In 1908, one of her reports included a note that simply stated, “The brighter variables have the longer periods” (Leavitt et al. 1908). In her typical humble style, she was simply trying to relay the facts and not over-interpret the data. However, the implications were immediately obvious: because the stars she was observing were all in the Magellanic Clouds, they were all about the same distance from Earth (Mitchell 1976). If the correlation she uncovered was in fact correct, a star’s absolute brightness (luminosity) could be gleaned from determining its period. Then comparing this absolute luminosity with its apparent brightness will yield the distance (Mitchell 1976). Knowing the distance would then be a major piece of the puzzle to solve the great question about nebulae and whether or not they are beyond the Milky Way galaxy. More data was needed to confirm this hypothesis.
Figure 5. The Period-Luminosity relationship observed by Henrietta Leavitt (Mitchell 1976)
Unfortunately, soon after her report was published, she fell ill and returned to stay with her parents who were now in Wisconsin (Bartusiak 2009). Since was gone for so long and because Pickering so valued her work, a box of plates was shipped to her so she could examine them while recovering (Bartusiak 2009). She finally made it back to Harvard in 1910 after a year and half absence, but almost immediately had to leave again when father passed away (Bartusiak 2009). She eventually got back to the observatory and published her latest results in the 1912 Harvard Circular. The report boldly stated, “A remarkable relation between the brightness of these variables and the length of their periods will be noticed” (Leavitt et al. 1912). In other words, brighter stars have longer periods. The stars measured are known as Cepheid variables because the first of its type was found in the constellation Cepheus (Johnson 2005). This new Cepheid yardstick (i.e., Henrietta’s law) could be used to determine the relative distances between stars (Johnson 2005). Now all that was needed was the distance to the closest star in order to calibrate this yardstick.
The technique used to measure the distance to the closest stars is known as parallax (Johnson 2005). This involves measuring the angle to a star at a certain time and then measuring it again precisely six months later when the Earth is on the other side of the Sun (Johnson 2005). Stars that are relatively close will appear to move in relation to the further away background star similar to the way one’s extended thumb appears to move in relation to background objects when one alternately blinks his eyes. Although simple in theory, this technique is difficult to implement in practice due to the enormous distances of the stars and the precision instruments required to detect their motion (Johnson 2005). After several attempts, the American astronomer Henry Norris Russell used parallax to put the distance of the Small Magellanic Cloud at 80,000 light years, a truly mind blowing number at the time (Johnson 2005). Russell wrote to his colleague Ejnar Hertzsprung, “I had not thought of making the very pretty use you make of Miss Leavitt’s discovery about the relation between period and absolute brightness. There is of course a certain element of uncertainty about this, but I think it is a legitimate hypothesis” (Johnson 2005). Thanks to Henrietta Swan Leavitt, astronomy finally had a way to measure beyond the closest stars and determine if there were objects beyond the Milky Way.
Figure 6. A typical report of new variables in the Harvard Circular (Leavitt 1913)
Unfortunately, despite her invaluable contribution, Henrietta continued to toil away in obscurity as a glorified computer. This did not deter her efforts as she continued to not only amass data, but also provide details notes about biases and uncertainties. For example, she wrote about the uncertainty in her measurements, “It is evident that, owing to the small range of the variable and the difficulty of estimating the magnitude of so bright an object, the observations are not sufficiently precise to permit a further correction to the period” (Leavitt et al. 1914). Johnson (2005) wrote, “It was work to take pride in. Ph.D.s have been awarded for less.” Astronomer Harlow Shapley admired Henrietta’s work and used it to calibrate the size of the Milky Way in order to debate the theory of “island universes.” This was the idea that the Milky Way was just one of many galaxies throughout the universe. Of Henrietta, Shapley wrote, “Her discovery of the relation of period to brightness is destined to be one of the most significant results of stellar astronomy” (Johnson 2005). After he assumed leadership of the Harvard observatory following Pickering’s death, Shapley called Henrietta, “one of the most important women ever to touch astronomy.” Tragically, Henrietta would not live long enough to see all the fruits her discovery would be bear as she passed away on December 12, 1921 (Johnson 2005).
As a consequence, it is vitally important that Henrietta Swan Leavitt’s importance to the field of astronomy be recognized. According to Johnson (2005), Henrietta Swan Leavitt’s story has “slipped through the cracks.” Perhaps this is because she never married and died young (Johnson 2005). Another reason could be her solemn Puritanical nature. In her obituary, a colleague wrote:
“Miss Leavitt inherited, in a somewhat chastened form, the stern virtues of her puritan ancestors. She took life seriously. Her sense of duty, justice and loyalty was strong. For light amusements she appeared to care little. She was a devoted member of her intimate family circle, unselfishly considerate in her friendships, steadfastly loyal to her principles, and deeply conscientious and sincere in her attachment to her religion and church.” (Johnson 2005).
Henrietta accomplished her work during a time when astronomy was decidedly dominated by males. Even the scant praise she earned was somewhat hollow as it condescendingly described women as being adept at detailed work, but affirmed that more difficult think matters were best suited for men (Johnson 2005). Despite all of this, she endured unflinchingly and led the way for refining the astronomical yardstick. Unlike some of her colleagues, Henrietta left behind little in the form of personal writings that would give some clue as to her feelings about her status in the field. Instead, she left behind a wealth of data and meticulous notes that enabled other astronomers to unlock the mysteries of the universe. Even to this day, astronomers are still refining her period-luminosity relationship, particularly the influence of metallicity (Garcίa-Varela 2013).
The h-index is a way of quantifying an individual’s research impact. According to Harzing (2007), Henrietta is credited with authorship of thirty-nine articles and has received 319 citations for an average of 8.18 citations per paper giving her an h-index of 4. For comparison, Henry McEwen was an amateur astronomer during the same time period wrote 89 papers, received 1119 citations (12.57 citations per paper), giving him a h-index of 16 (McKim 2005 & Harzing 2007). This may paint Henrietta’s contribution as low until we look at the two Harvard observatory directors whose careers she most powerfully influenced: Pickering’s h-index of 28 and Shapley’s h-index of 30 are incredibly high. It is difficult, if not impossible, to assess Henrietta Swan Leavitt’s importance using traditional metrics. She was not technically an astronomer, but rather a “skilled laborer” at the observatory (Johnson 2005). Consequently, while she did submit her data in the observatory’s bulletin, she rarely submitted in the more prestigious astronomical journals. Nevertheless, she was undoubtedly an astronomer in the purest sense of the word: she took observations and looked for underlying phenomena to predict future astronomical events. She understood that the discovery was the important thing, not the discoverer (Johnson 2005). Everyone interested in astronomy should know not only about the role Cepheid variables on the distance ladder, but also about the remarkable woman who unlocked their secret.
References
Bartusiak, M. 2009, Natural History, 118, 14-17
Burleigh, R. 2013, Look Up!, (New York: Simon & Schuster)
Garcίa-Varela et al. 2013, MNRAS, 431, 2278-2284
HARVARDweb: http://dasch.rc.fas.harvard.edu/telescopes.php accessed 29 August 2014
Harzing, A. W. 2007, http://www.harzing.com/pop.htm
Johnson, G. 2005, Miss Leavitt’s Stars, (New York: W.W. Norton & Co.)
Leavitt, H. et al. 1908, Annals of Harvard College Observatory, 60, 87-108
Leavitt, H. et al. 1912, Harvard College Observatory Circular, 173, 1-3
Leavitt, H. et al. 1913, Harvard College Observatory Circular, 179, 1-4
Leavitt, H. et al. 1914, Harvard College Observatory Circular, 186, 1-4
McKim, R. 2005, JBAA, 115, 13
Mitchell, H. 1976, The Physics Teacher, 14, 162-167
Nelson, S. 2008, Nature, 455, 36-37
Singh, S. 2004, New Scientist, 184, 54-55
Subscribe to:
Comments (Atom)












